Welcome 20 divided by 8 to our blog! Today, we are diving into the world of division and exploring how to get the most out of dividing 20 by 8. Division may seem like a daunting task at first, but fear not! We have got you covered with tips, tricks, and practical applications that will leave you feeling like a division pro. So grab your calculators and let’s dive right in!
Understanding the basics of division
Understanding the basics of division is essential for tackling any division problem, including dividing 20 by 8. Division is simply the process of splitting a number into equal parts or groups. It allows us to distribute quantities evenly and find out how many times one number can be divided by another.
To visualize division, think of it as sharing items among a certain number of people. For example, if you have 20 cookies and want to divide them equally among 8 friends, you would need to determine how many cookies each person will receive.
In mathematical terms, we express this as 20 ÷ 8. The dividend (the number being divided) is 20 and the divisor (the number we are dividing by) is 8. The quotient represents the result of the division operation – in this case, how many cookies each friend will receive.
It’s important to remember that not all numbers divide evenly. In some cases, there may be a remainder when dividing two numbers. This occurs when one quantity cannot be distributed equally among others.
Having a solid understanding of these basic concepts sets the foundation for solving more complex division problems later on. So let’s move on to exploring different ways to solve 20 divided by 8!
Different ways to solve 20 divided by 8
Have you ever wondered how to solve the division problem 20 divided by 8? Well, you’re in luck because there are actually different ways to approach this calculation. Let’s explore some of these methods and see which one works best for you.
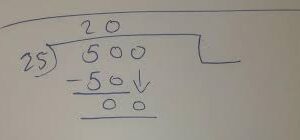
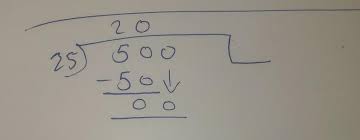
One way to solve 20 divided by 8 is through long division. Start by dividing the first digit of the dividend (which is 2) by the divisor (which is also 2). The result is 1, so write down a “1” above the line. Then multiply this result (1) with the divisor (8), giving us 8. Subtract this product from the first digit of our dividend, resulting in a remainder of “12”. Bring down the next digit from our dividend, which is “0”, and repeat the process until we have no more digits left.
Another method to tackle this division problem is through estimation. Round both numbers involved in your calculation – that means rounding up or down depending on their value – and then divide them as if they were whole numbers without any decimals or remainders.
If precision isn’t your highest priority, another option could be using mental math tricks such as fractional approximation or simplification techniques. In this case, we can simplify both numbers before dividing them: since both numbers are divisible by two, divide each number by two separately before performing the final division operation.
As you can see, there are multiple approaches to solving a simple division problem like 20 divided by eight! Choosing which method suits you best will depend on your preference and situation at hand.
The importance of simplifying fractions
Simplifying fractions may seem like a small and insignificant step in the division process, but its importance should not be underestimated. When we simplify a fraction, we reduce it to its lowest terms by dividing both the numerator and denominator by their greatest common divisor. This not only makes our calculations easier but also helps us to understand the relationship between different parts of the fraction.
One key benefit of simplifying fractions is that it allows us to work with smaller numbers, making calculations more manageable. For example, when solving 20 divided by 8, simplifying the fraction would give us 5/2 instead of 10/4. Working with smaller numbers can save time and minimize errors during complex division problems.
In addition to practical benefits, simplifying fractions also aids our understanding of proportions and ratios. By reducing a fraction to its simplest form, we can see how different quantities relate to each other more clearly. This is particularly valuable in real-world applications such as cooking recipes or measuring ingredients where accurate proportions are essential for successful outcomes.
Moreover, simplified fractions make it easier for us to compare and order values accurately. When dealing with multiple fractions or mixed numbers, having them all expressed in their simplest forms allows for quick comparisons without needing additional conversions or calculations.
Simplifying fractions is an important skill that enhances both computational efficiency and mathematical comprehension. It paves the way for smoother problem-solving experiences while increasing our ability to grasp proportional relationships in various contexts
Tips for tackling more complex division problems
Tackling more complex division problems can seem daunting at first, but with a few helpful tips and strategies, you can approach them with confidence. Here are some pointers to keep in mind when faced with trickier divisions.
It’s important to break down the problem into smaller, more manageable steps. Look for any patterns or relationships within the numbers involved that could simplify the calculation. For example, if there are common factors between the dividend and divisor, consider dividing both by their highest common factor before proceeding.
Additionally, exploring alternative methods of solving division problems can be beneficial. One technique is long division – a methodical process that allows you to work through each step of the division systematically. Another approach is using estimation or rounding techniques to arrive at an approximate answer quickly.
Another useful tip is to practice mental math skills regularly. Strengthening your ability to perform quick calculations mentally will save time and make tackling complex divisions easier.
Furthermore, don’t hesitate to use visual aids such as diagrams or charts if they help you understand the problem better. Sometimes seeing a visual representation of numbers can provide clarity and assist in finding solutions.
Perseverance and patience are key when faced with challenging division problems. It’s okay if you don’t immediately grasp how to solve them – take your time and try different approaches until you find one that works for you.
By applying these tips and developing your problem-solving skills over time, even the most complex division problems will become more manageable!
Practical applications of knowing how to divide
Practical applications of knowing how to divide extend far beyond the confines of a math classroom. In fact, division is a fundamental operation that we encounter in various aspects of our everyday lives.
One practical application of division is when it comes to dividing resources or quantities. For example, if you have 20 cookies and want to distribute them equally among 8 friends, knowing how to divide allows you to ensure everyone gets their fair share. This concept applies not only to cookies but also to money, time, and other divisible entities.
Another real-world application lies in cooking and baking. Recipes often call for measurements that need to be divided or multiplied depending on the desired serving size. Understanding division allows you to accurately adjust ingredient quantities without compromising on taste or consistency.
Division also plays a role in budgeting and financial planning. Being able to divide income into different categories such as savings, expenses, and investments helps individuals manage their finances effectively. Moreover, understanding division enables us to calculate percentages for discounts or sales tax when shopping.
In fields like architecture and construction, dividing spaces into equal parts is crucial for creating balanced designs with proper dimensions. Without this skill, buildings could lack functionality and aesthetic appeal.
Furthermore, knowledge of division becomes invaluable when sharing items between multiple people or groups—for instance during team projects at work or allocating resources during disaster relief efforts.
These are just a few practical examples showcasing the importance of knowing how to divide in our daily lives outside the realm of mathematics class. Whether it’s sharing cookies with friends or managing budgets effectively—division skills prove indispensable across diverse situations!
How to use a calculator for division
How to Use a Calculator for Division
Using a calculator can be incredibly helpful when it comes to solving division problems quickly and accurately. Here are some simple steps to follow:
1. Turn on your calculator and make sure it’s set in the “standard” mode or “calculator” mode.
2. Enter the dividend, which is the number you want to divide (in this case, 20).
3. Press the division symbol (/) on your calculator.
4. Enter the divisor, which is the number you are dividing by (in this case, 8).
5. Press the equals (=) button on your calculator.
6. The quotient will be displayed on your screen, giving you the answer to 20 divided by 8.
Remember that calculators can handle more complex division problems as well! If you have a decimal quotient or repeating decimals in your answer, make sure your calculator is capable of displaying those types of results.
Using a calculator for division not only saves time but also reduces errors that might occur when doing long divisions manually. So next time you encounter a tricky division problem, don’t hesitate to grab that trusty calculator and let it do all the hard work for you!
Conclusion
Conclusion
Understanding the basics of division is essential for solving mathematical problems and everyday situations that require dividing quantities. In this article, we have explored various ways to get the most out of dividing 20 by 8.
By breaking down the process of division into manageable steps, we can approach more complex problems with confidence. Simplifying fractions allows us to work with smaller numbers, making calculations easier and more efficient.
Knowing how to divide has practical applications in many areas of life. Whether you’re splitting a bill among friends or scaling ingredients for a recipe, division skills come in handy. Additionally, understanding division lays the foundation for higher-level mathematics and problem-solving abilities.
While mental math can be useful for simple divisions like 20 divided by 8, calculators are valuable tools when dealing with larger numbers or decimals. Learning how to use a calculator effectively can save time and reduce errors in calculations.
Mastering the fundamentals of division empowers us to solve mathematical problems accurately and efficiently. From everyday scenarios to advanced mathematics, knowing how to divide opens up endless possibilities for growth and success. So keep practicing your division skills as they will continue to serve you well throughout your academic journey and beyond!