Are 180 divided by 4 you ready to unlock the mysteries of division? If so, you’ve come to the right place! Division is a fundamental mathematical operation that allows us to split numbers into equal parts. From solving everyday problems to understanding complex concepts, division plays a crucial role in our lives. In this blog post, we will delve into the world of division and explore one specific equation: 180 divided by 4. Get ready for some mind-boggling math as we break it down step-by-step and discover its practical applications. So grab your thinking cap and let’s dive in!
What is Division?
Imagine you have a basket filled with 180 apples, and you need to divide them equally among 4 friends. This is where division comes into play. Division is a mathematical operation that allows us to distribute or split numbers into equal parts.
At its core, division is all about sharing and dividing things fairly. It helps us solve problems involving quantities that need to be distributed evenly among a certain number of groups or individuals.
When we perform division, we are essentially asking the question: “How many times does one number fit into another?” In our example, we are asking how many times 4 (representing the friends) can go into 180 (representing the apples).
To visualize this concept, think of division as separating a whole into smaller pieces. Each piece represents an equal share. The quotient obtained from the division process gives us the size of each individual share.
Division can be represented using various symbols or notations, but one commonly used symbol is ÷ (a forward slash with dots above and below it). So when you see something like “180 ÷ 4,” it means we’re trying to divide 180 by 4.
Now that we understand what division is at its core, let’s dive deeper and explore how exactly we perform divisions step-by-step in the next section!
Understanding the Division Symbol
Understanding the Division Symbol
Division is a fundamental mathematical operation that involves splitting a number or quantity into equal parts. It allows us to distribute objects, money, or even time in an organized way. The division symbol, denoted by ÷ or /, represents this operation.
When we see the division symbol, it tells us that we need to separate a given value into smaller groups of equal size. For example, if you have 12 apples and want to divide them equally among 4 friends, each friend would receive 3 apples.
To perform division correctly, it’s important to follow some basic rules. First, identify the dividend (the number being divided) and divisor (the number dividing the dividend). Next, divide the dividend by the divisor and determine how many times the divisor can fit into the dividend evenly.
For instance, when dividing 180 by 4 using long division method: place 4 outside and start with 1 as quotient. Multiply 1 with divisor which gives us our first product as ‘4’. Subtract this from current value inside – in this case its ‘8’.
Continue this process until you reach zero or find remainder! This will help you solve complex divisions too!
By understanding how to apply these steps correctly when working with numbers like 180 divided by 4 ensures accurate results are achieved every time.
Stay tuned for more examples on real-life applications of division!
How to Divide Numbers: Step-by-Step Guide
Division is a fundamental mathematical operation that involves splitting or distributing a number into equal parts. It is an essential skill to learn, as it helps us solve problems and understand the relationship between numbers. To divide numbers, we follow a step-by-step guide:
1. Identify the dividend (the number being divided) and the divisor (the number dividing the dividend).
2. Begin with the leftmost digit of the dividend and divide it by the divisor.
3. Write down how many times the divisor goes into that digit above or beside it.
4. Multiply this quotient by the divisor and subtract it from that part of the dividend.
5. Bring down the next digit of your original dividend and repeat steps 2-4 until you have no more digits.
By following these steps, you can divide any two numbers efficiently and accurately.
Understanding how to divide numbers has practical applications in various real-life situations, such as sharing equally among friends or calculating prices per unit when shopping for groceries.
Mastering division also enables us to solve more complex math problems involving fractions, decimals, ratios, proportions, and percentages. It forms a strong foundation for higher-level math concepts like algebra and calculus.
In conclusion,
Learning how to divide numbers using a step-by-step guide is crucial for developing basic math skills while paving the way for advanced mathematical understanding later on in life. So practice regularly, be patient with yourself as you learn new concepts along your mathematical journey!
Real-Life Examples of Division
Real-Life Examples of Division
Division is not just a concept that exists in textbooks or classrooms; it has practical applications in our everyday lives. Let’s explore some real-life examples where division plays a crucial role.
One common example involves dividing food among friends or family members. Imagine you have four slices of pizza and want to divide them equally among two people. By using division, each person would receive two slices.
Another scenario where division is used is when calculating the cost per item at the grocery store. Let’s say you need to buy 180 apples and they come in packs of 4. By dividing 180 by 4, you can determine that you will need to purchase 45 packs of apples.
Division also comes into play when planning events or organizing schedules. If you have a team of ten people working on a project for five days, dividing the workload evenly ensures everyone knows their tasks and deadlines.
In construction, division helps calculate measurements accurately. For instance, if you’re building a wall with bricks measuring 2 feet long and your desired length is 12 feet, dividing the length by the size of one brick (6) gives you an estimate of how many bricks are needed (2).
These are just a few examples showcasing how division plays an essential role in various aspects of our daily lives. Whether it’s sharing food, managing finances, organizing time or constructing something new – understanding and applying division helps us solve problems efficiently without leaving anyone behind!
The Concept of Remainders in Division
The concept of remainders in division is an important aspect to understand when dealing with numbers. When we divide one number by another, there are two possible outcomes: either the division is exact and there is no remainder, or there is a remainder.
To clarify this concept further, let’s take an example. Suppose you have 10 cookies and want to share them equally among 3 friends. Each friend will get 3 cookies, but there will be one cookie left over as a remainder. This remaining cookie cannot be divided equally amongst the friends.
Remainders can also be seen in larger divisions. For instance, if we divide a number like 37 by 5, the quotient would be 7 with a remainder of 2. This means that after dividing as much as possible (in this case getting seven groups of five), we are left with two extra units that cannot form another complete group.
Understanding remainders helps us determine how many whole groups can be formed during division and what remains afterwards. It allows us to accurately represent real-life situations where things may not divide evenly.
By grasping the concept of remainders in division, it enables us to solve problems involving sharing items equitably or distributing quantities fairly among different individuals or groups. Moreover, it lays the foundation for more advanced mathematical concepts such as fractions and decimals.
In conclusion,
the concept of remainders in division plays a crucial role in understanding how numbers interact when divided into groups or distributed evenly among people or objects.
180 divided by 4: Solving the Equation
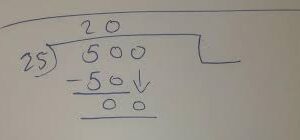
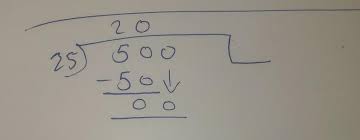
When faced with the equation 180 divided by 4, we need to find out how many times 4 can go into 180. Let’s break it down step-by-step.
First, we start with the number at hand, which is 180. We divide this number by the divisor, which in this case is 4.
To begin solving the equation, we ask ourselves: How many times does 4 fit into 18? The answer is four. So now we have a partial quotient of four.
Next, we subtract our product from the original dividend: 18 – (4 x 4) =2
Now, bring down the next digit of our dividend, which in this case is zero. So now our new number becomes “20”.
We repeat the process: How many times does 4 fit into twenty? The answer is five. Our updated partial quotient becomes “45”.
Subtracting once again: (20 – (5 x 4)) =0
At this point, there are no more digits left to bring down and divide. We have reached an even solution without any remainder.
Therefore, when dividing 180 by four equals forty-five! By following these simple steps and avoiding common errors mentioned earlier on your journey through division will lead you towards success every time
Common Mistakes to Avoid in Division
Common Mistakes to Avoid in Division
When it comes to division, there are a few common mistakes that people often make. One of the most frequent errors is forgetting to double-check their work. It’s easy to get caught up in the process and overlook simple arithmetic errors. Taking a moment to review your calculations can help you catch any mistakes before they become problematic.
Another mistake many individuals make is not fully understanding the concept of remainders. In some division problems, there will be numbers leftover after dividing evenly. These remainders should not be ignored or dismissed as unimportant but rather acknowledged and included in the final answer.
One key point to remember when dividing numbers is not assuming that larger dividends result in larger quotients. This misconception can lead to incorrect answers and confusion. Always approach each division problem with an open mind, regardless of the size of the numbers involved.
Additionally, using mental math without writing down intermediate steps may increase the likelihood of making errors. While mental math can be efficient for simple divisions, it’s crucial to write out each step for more complex problems.
Rushing through division problems without taking time for careful consideration often leads to careless mistakes and inaccuracies. Slow down and take your time; accuracy is far more important than speed when it comes to division.
By being aware of these common pitfalls and actively working on avoiding them, you’ll improve your overall proficiency in division calculation while reducing potential errors along the way.
Practical Applications of Knowing about 180 divided by 4
Practical Applications of Knowing about 180 divided by 4:
Understanding the concept of division and being able to solve equations like 180 divided by 4 may seem like a purely mathematical skill, but its applications extend far beyond the classroom. In fact, division is used in various real-life scenarios where we need to distribute or allocate resources efficiently.
For instance, consider a situation where you have 180 cookies that need to be shared equally among four friends. By knowing how to divide 180 by 4, you can ensure that each friend receives their fair share of delicious treats – a valuable skill when it comes to sharing and fairness!
Division also plays a crucial role in fields such as finance and budgeting. Let’s say you have $180 and want to split it evenly into four savings accounts. Knowing how much money should go into each account (which can be found through dividing $180 by 4) helps maintain an organized financial plan.
Furthermore, understanding division allows us to calculate rates and proportions accurately. For example, if you know that a car travels at an average speed of 45 miles per hour and wants to determine how long it takes for the car to cover a distance of 180 miles, dividing the total distance by the rate gives you the answer – in this case, it would take approximately four hours.
In cooking or baking recipes, knowing how much each ingredient contributes is essential for successful results. If a recipe calls for dividing quantities amongst servings or adjusting measurements based on different serving sizes (such as converting ingredients for two people instead of four), understanding division becomes invaluable.
The practical applications of knowing about division extend beyond these examples mentioned above; they permeate many aspects of our daily lives without us even realizing it. From splitting bills with friends at restaurants or determining fair distributions during team projects at work – having strong skills in division ensures efficiency and accuracy.
So next time you encounter situations involving equal sharing, financial planning, rate calculations, or even cooking and baking, remember the fundamental concept of
Conclusion
Conclusion
Understanding and being able to perform division is an essential skill in mathematics. It allows us to divide quantities into equal parts, solve real-life problems, and make sense of numbers in the world around us.
In this article, we have explored the concept of division, how to divide numbers using a step-by-step guide, and examined real-life examples to illustrate its practical applications. We also solved the equation 180 divided by 4 together and discussed common mistakes to avoid.
By knowing about 180 divided by 4, we can better understand fractions, percentages, ratio calculations, budgeting, and many other areas where dividing quantities is necessary. This knowledge empowers us with a foundational tool for problem-solving in various fields such as finance, science, engineering, or even everyday tasks like splitting bills among friends.
Remember that practice makes perfect when it comes to division. The more you work on dividing different numbers using various methods and strategies learned today; the more confident you will become in tackling complex mathematical problems effortlessly.
So continue exploring division with curiosity and embrace its power as a fundamental mathematical operation that opens up new possibilities for understanding our world.