Are what is the fraction for .67 you ready to unlock the mystery of fractions? Whether you’re a math enthusiast or someone who shudders at the thought of numbers, understanding fractions is an essential skill. They are not just abstract concepts confined to textbooks; they play a crucial role in our everyday lives. So, if you’ve ever wondered what fraction represents the decimal .67, then keep reading! In this blog post, we’ll dive into the world of fractions and explore how decimals can be converted into these fascinating mathematical entities. Get ready to discover the magic behind .67 and its equivalent fraction. Let’s embark on this numerical journey together!
Understanding fractions
Fractions…they may seem like a daunting concept, but fear not! Understanding fractions is simpler than you might think. At its core, a fraction represents a part of a whole. Think of it as slicing up your favorite pizza into equal-sized pieces. Each slice is a fraction, showing how much of the whole pizza you have.
Now let’s break down the components of a fraction. You have the numerator and denominator. The numerator tells us how many parts we have, while the denominator represents the total number of equal parts that make up the whole.
Fractions come in different forms – proper fractions (where the numerator is smaller than the denominator), improper fractions (where the numerator is larger than or equal to the denominator), and mixed numbers (which combine whole numbers with fractions).
Understanding fractions allows us to compare quantities and perform mathematical operations like addition, subtraction, multiplication, and division. They are used in various real-life scenarios such as cooking recipes, measurements, financial calculations, and even sports statistics!
So remember, don’t be intimidated by fractions! Embrace them as powerful tools that help us make sense of our numerical world. With this foundational understanding in place, we can now explore how decimals can be transformed into their fractional counterparts – including finding out what fraction corresponds to .67!
Representation of fractions
Fractions are a fundamental concept in mathematics and play a crucial role in our everyday lives. They represent parts of a whole, allowing us to express quantities that are not whole numbers. Understanding how fractions are represented is essential for grasping their meaning and applying them effectively.
In mathematical notation, fractions are typically written as one number (the numerator) divided by another number (the denominator), separated by a horizontal line. For example, 1/2 represents one-half of something or dividing an object into two equal parts.
Fractions can also be represented visually using shapes such as circles or rectangles. By dividing these shapes into equal parts and shading the appropriate portion, we can visualize the fraction’s value. This visual representation helps us better understand the relationship between the numerator and denominator.
Another way to represent fractions is through decimal notation. Decimals are often used in practical applications where precision is required; however, they can be converted back to fractions if needed. Converting decimals to fractions involves identifying patterns or repeating sequences in the decimal representation.
Understanding different representations of fractions allows us to work with them more flexibly and apply them in various situations accurately. Whether it’s measuring ingredients for a recipe or calculating percentages at work, knowledge of fractions empowers us to make precise calculations and solve real-world problems efficiently without losing any significant information along the way
Converting decimals to fractions
Converting decimals to fractions can be a useful skill to have in various situations. It allows us to express decimal numbers as more familiar and easily understood fractions. To convert a decimal to a fraction, we need to understand the relationship between the digits after the decimal point.
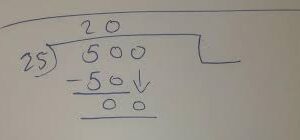
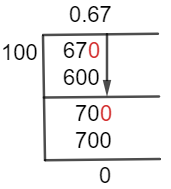
The first step is identifying the place value of the last digit after the decimal point. For example, in the number 0.67, 7 is in the hundredth place because it is two digits after the decimal point.
Next, we write down this digit as our numerator and determine our denominator based on its place value. Since 7 is in the hundredth place, our denominator will be 100.
So for 0.67, its equivalent fraction would be 67/100.
To simplify this fraction further, we can divide both numerator and denominator by their greatest common divisor (GCD). In this case, both numbers are divisible by 1 so there are no further simplifications possible.
Converting decimals to fractions opens up possibilities for understanding and working with numbers in different ways. Whether it’s calculating measurements or solving mathematical problems, having a grasp on converting decimals can come in handy!
Remember practice makes perfect when it comes to converting decimals into fractions!
Finding the fraction for .67
Finding the fraction for a decimal number can be a useful skill to have. It allows us to represent numbers in a different way, providing more flexibility and precision in our calculations. When it comes to .67, we can easily find its corresponding fraction.
To convert a decimal into a fraction, we look at the place value of the digits after the decimal point. In this case, 67 is in the hundredths place since it has two digits after the decimal point. So, we can express .67 as 67/100.
This fraction may seem complex at first glance, but it’s important to remember that fractions are all about simplifying and finding their simplest form. To simplify 67/100, we divide both numerator (the top number) and denominator (the bottom number) by their greatest common divisor (GCD), which is 1 in this case.
So there you have it! The simplified fraction for .67 is simply 67/100. This means that if you have .67 of something, you actually have sixty-seven hundredths of that whole thing.
Understanding how decimals relate to fractions opens up new possibilities when working with numbers. From measurements and proportions to financial calculations and even cooking recipes – fractions and decimals play an integral role in various real-life applications.
In conclusion,
finding the fraction for .67 gives us another way to represent this decimal value accurately: 67/100.
Simplifying the fraction
When it comes to fractions, simplicity is key. Simplifying a fraction means reducing it to its smallest possible form by dividing both the numerator and denominator by their greatest common divisor. This process allows us to express fractions in a way that is easier to understand and work with.
To simplify a fraction, we need to find the greatest common divisor (GCD) of the numerator and denominator. This can be done by determining the factors of both numbers and finding their highest common factor.
For example, let’s take .67 as our decimal value. To convert this decimal into a fraction, we multiply it by 100 to get rid of the decimal point: 0.67 * 100 = 67/100.
Now, let’s simplify this fraction. The GCD of 67 and 100 is 1 since there are no other common factors between them besides 1 itself. Therefore, we divide both the numerator and denominator by 1:
(67 ÷ 1) / (100 ÷ 1) = 67/100
And voila! We have simplified our fraction.
Simplifying fractions not only makes them easier to work with mathematically but also helps us grasp their meaning more intuitively in real-life scenarios such as recipe measurements or financial calculations.
Understanding how to simplify fractions allows us to make sense of relationships between different quantities and ensure accuracy in various applications involving numerical values.
Real-life applications of fractions and decimals
Real-life applications of fractions and decimals can be found all around us, even if we don’t always realize it. One common application is when we go shopping and need to calculate a discount or figure out the final price after tax. We use fractions and decimals to determine how much money we will save or spend.
Another real-life scenario where fractions and decimals come into play is in cooking and baking. Recipes often call for measurements such as half a cup or one-fourth teaspoon. Understanding these fractional quantities is essential for creating delicious dishes.
Fractions are also used in construction and measurement. Architects rely on precise measurements to design buildings, while carpenters use them to cut materials accurately. Decimals are crucial in scientific research, where precise calculations may involve small increments or decimal places.
In finance, understanding fractions allows us to comprehend interest rates, percentages, and stock market fluctuations more effectively. Investors analyze data presented as decimals to make informed decisions about buying or selling stocks.
Furthermore, sports enthusiasts encounter fractions when analyzing player statistics like batting averages in baseball or shooting percentages in basketball.
In conclusion (This section doesn’t require a conclusion), fractions and decimals have practical implications beyond the classroom setting. They play an integral role in various aspects of our everyday lives – from calculating discounts at the store to designing buildings – making them essential tools for problem-solving across different fields
Conclusion
Conclusion
Fractions are an essential concept in mathematics that allow us to represent parts of a whole. They provide a way to express numbers that are not whole or integers, such as decimal numbers. In this blog post, we explored the process of finding the fraction for the decimal number .67.
By converting .67 into a fraction, we discovered that it can be represented as 67/100. This means that .67 is equal to sixty-seven hundredths. We also simplified the fraction by dividing both the numerator and denominator by their greatest common divisor, resulting in 2/3.
Understanding fractions and decimals has practical applications in various aspects of our lives. From cooking recipes where precise measurements are crucial to financial calculations involving percentages and interest rates, fractions and decimals play a significant role.
So next time you come across a decimal like .67, remember that it can be expressed as the fraction 2/3. Embrace your knowledge of fractions and decimals; they have many real-life implications!